Na jednej z rozmów kwalifikacyjnych dostałem zadanie stworzenia algorytmu który pomoże w znalezieniu początku pętli na liście wskaźnikowej jednokierunkowej. Przyznam, że pytanie stanowiło dla mnie nie małe wyzwanie. Po dłuższym zastanowieniu napisałem kod, który przechodząc przez kolejne elementy naszej listy porównuje czy dany element jest już na liście tymczasowej, jeśli nie to zrzuca go na nią i podąża dalej. Rozwiązanie było, niezbyt szybkie i ładne lecz działało. Problem pojawił się gdy rekruter dodał – co w przypadku gdy lista zawiera ogromne ilości elementów? Jak by to Pan zoptymalizował? Niestety jak to bywa, nie udało mi się wtedy niestety udoskonalić tego algorytmu. Problem ten nurtował mnie na tyle, że po powrocie do domu zacząłem poszukiwać odpowiedzi w notatkach i książkach z algorytmów, które zostały mi po studiach. Okazało się, że na jeden z wykładów musiałem zaspać. Podczas poszukiwań natrafiłem na rozwiązanie zwane techniką „biegacza”.

Na czym to polega?

Technika owa polega na wykorzystaniu dwóch wskaźników, wolnego i szybkiego. Podczas przechodzenia przez listę wolny wskaźnik przechodzi ją co jeden element, natomiast szybki wskaźnik porusza się co dwa elementy. Okazuje się że takie poruszające się wskaźniki w razie wystąpienia pętli zawsze spotkają się na którymś ze znajdujących się w niej elementów. Nam zostaje tylko porównywać elementy, na które wskazują oba wskaźniki podczas poruszać się po liście. W przypadku gdy elementy są takie same wiem już że w liście występuje pętla.

Jak już dwa takie wskaźniki spotkają się na jednym elemencie listy jeden ze wskaźników przestawiamy z powrotem na początek listy. Drugi wskaźnik pozostaje na elemencie, na którym nastąpiło poprzednie spotkanie. Puszczamy ponownie przechodzenie po liście z tą różnicą, że oba wskaźniki przestawiamy o jeden element w każdym kroku. Kolejne miejsce spotkania wskaźników wskaże nam błędny element listy, na którym pętla ma swój początek.

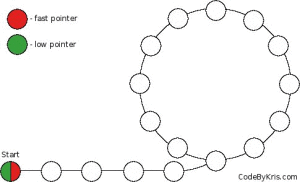
Poniżej umieściłem rysunek ilustrujący kolejne kroki algorytmu:

 

 

 

Reasumując nasz algorytm będzie składał się z następujących kroków:

1. Utwórz dwa wskaźniki, szybki i wolny.
2. Przesuwaj wolny wskaźnik o jeden krok i szybki wskaźnik o dwa kroki po liście.
3. Gdy oba wskaźniki się spotkają przesuń wskaźnik wolny na początek listy. Wskaźnik szybki pozostaje na elemencie gdzie wskaźniki się spotkały.
4. Przesuwaj oba wskazni9ki o jeden krok aż do momentu kolejnego spotkania.
5. Zwróć punkt spotkania.

Kodujemy

Funkcja przedstawiona poniżej pobiera pierwszy element listy listy dwukierunkowej i zwraca nam element, który powoduje zapętlenie listy. W przypadku poprawnej listy funkcja zwróci null.

LinkedListNode<?> findTopOfLoop(LinkedListNode<?> head) {
        //tworzymy wolny i szybki wskaźnik 
	LinkedListNode<?> slow = head;
	LinkedListNode<?> fast = head;
		
        //znajdujemy element na którym następuje spotkanie wskaźników
	boolean isCollisionSpot = false;
	while(fast != null && fast.getNext() != null && !isCollisionSpot) {
		fast = fast.getNext().getNext();
		slow = slow.getNext();
			
		if(fast == slow) {
			isCollisionSpot = true;
		}
	}
	
        //wskaźniki nie spotkały się, więc pętla nie wystepuje	
	if(fast == null || fast.getNext() == null) {
		return null;
	}
	
        //przestawiamy jeden z wskaźników na początek listy
        //oba wskaźniki znajdują się w tej samej liczbie kroków od miejsca wystąpienia pętli	
        //poruszamy wskaźniki o jeden krok aż do miejsca spotkania
	slow = head;
	while (fast != slow) {
		fast = fast.getNext();
		slow = slow.getNext();
	}
		
	return fast;
}

Troszkę matematyki…

Podwaliny matematyczne danego problemu zawsze zostawiam na koniec. Zawsze lubię uczyć się od tyłu, analizując już gotowe rozwiązanie, poznać zasady działania, by na końcu móc już na luzie zająć się podstawami na jakich ono jest oparte. Tam metoda pozwala mi szybciej przyswoić sobie, czasami trudne i przypominające na pierwszy rzut oka bełkot, dowody matematyczne.

Jeśli nie lubicie czytać wywodów matematycznych możecie pominąć ten rozdział. Osobiście uważam, że mimo nudy jaką powiewa w czasie takich wywodów warto się zagłębić w tą tematykę, choć by ze względu na to, że możemy poznać podstawy na jakich bazuje algorytm. Niektórym osobom pomaga to zapamietać rozwiązanie.

Na początek udowodnimy, że dwa wskaźniki muszą się kiedyś spotkać w pętli. Gdy przymniemy, że wskaźnik wolny w danym kroku był na pozycji k (krok) a wskaźnik szybki na k + 1. Cofając się w czasie, w poprzednim kroku wskaźnik wolny musiał być na pozycji k – 1 a wskaźnik szybki na pozycji (k + 1) – 2, co po uproszczeniu daje nam również k – 1. Jak widać wskaźniki spotkały się w kroku k – 1.

Rozgrzewkę mamy za sobą. Wiemy już że nasze wskaźniki spotkają się w pętli warto było by wskazać miejsce w którym to nastąpi.

Wiemy, że na każde i kroków wskaźnika wolnego wskaźnik szybki robi 2i kroków. Możemy założyć też również,  że na naszej feralnej liście jest fragment p (prawidłowy) kroków gdzie lista jest zbudowana poprawnie i nie występuje pętla. Czyli krok p można też uznać za początek pętli.

Łącząc te dwie informacje można zauważyć, ze gdy wskaźnik wolny dociera do początku pętli w p kroków to wskaźnik szybki jest już od niego oddalony o 2p kroków. Szybki wskaźnik przechodzi więc w tym samym czasie o 2p – p kroków więcej od wskaźnika wolnego co daje nam o p kroków dłuższą podróż.

Nasz pętla może być o wiele krótsza lub dłuższa niż odcinek przed pętlą więc wartość p musimy zapisać za pomocą wzoru mod(p, R) gdzie R to rozmiar pętli. W dalszej części dowodu wyrażanie mod(p, R) będziemy oznaczać jako P.

Dotarliśmy do punktu w którym nasz wolny wskaźnik stojąc na początku pętli zrobił 0 kroków po jej obwodzie. W tym samym czasie wskaźnik szybki wykonał ich w liczbie P. Gdy spojrzymy na położenie obu wskaźników względem siebie, to zauważymy, że wskaźnik wolny jest P kroków za szybkim natomiast wskaźnik szybki jest R – P przed wolnym.

Jeżeli ponownie wprawimy w ruch nasze wskaźniki to wskaźnik szybki będzie się zbliżał z szybkością jednego kroku na ruch do wskaźnika wolnego. Spotkanie nastąpi więc po R – P krokach, czyli P kroków przed początkiem pętli.

Dowiedzieliśmy się, że spotkanie wskaźników nastąpi zawsze P kroków przed początkiem pętli. Przyjęliśmy wcześniej że P = mod (p, R), a zgodnie z twierdzeniem o reszcie z dzielenia wychodzi nam wzór p = K + M * R, gdzie M to dowolna liczba.

Można więc przyjąć, że dla dowolnej liczby M spotkanie nastąpi zawsze p kroków od początku pętli. Dlatego punkt spotkania wskaźników jak i początek listy powiązanej (głowa listy) znajdują się p węzłów od początku pętli.

 

Mam nadzieje, że udało mi się przybliżyć wam drodzy czytelnicy technikę „biegacza” (czyli dwóch wskaźników ) i nie sprawi wam ona już żadnego problemu na rozmowie kwalifikacyjnej.